圆的内接四边形有哪些性质
的有关信息介绍如下: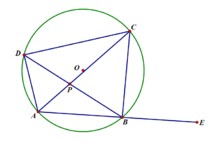
以上图所示圆内接四边形ABCD为例:
圆心为O,延长AB至E,AC、BD交于P,则:
圆内接四边形的对角互补:∠BAD+∠DCB=180°,∠ABC+∠ADC=180°
圆内接四边形的任意一个外角等于它的内对角:∠CBE=∠ADC
圆心角的度数等于所对弧的圆周角的度数的两倍:∠AOB=2∠ACB=2∠ADB
同弧所对的圆周角相等:∠ABD=∠ACD
圆内接四边形对应三角形相似:△ABP∽△DCP(三个内角对应相等)
相交弦定理:AP×CP=BP×DP
托勒密定理:AB×CD+AD×CB=AC×BD
来源:http://baike.baidu.com/link?url=KanMvsy392L9dUyaiOSx2YZAlLP5-Rvs2kw-ky2xVgNat15zGfVffdP9Qlg8lssNn8oYcN9TqZIjovpK6Y09klUiM1Rv6QIcYCM1Btu5cfGSYCEmDPOR-RX4Q7ECyvGhSfLuCLBXLmnXD-xxd2vzyK



